はじめに
今回の記事は、前回に引き続き、私が受講しているE資格 JDLA認定プログラムの「ラビットチャレンジ」のレポート記事です。
今回のテーマは深層学習です。
講座ではDay1〜Day4まで分かれており、今回はDay1に取り組みます。
Day1はニューラルネットワークについて主に扱います。
確認テストも併せて載せていきます。
ニューラルネットワークの全体像
機械学習や深層学習(ディープラーニング)を扱う上で、重要なのがニューラルネットワークです。
ニューラルネットワークとは、人間の脳内の神経細胞(ニューロン)とその繋がりを数式的モデルで表現したものです。
複雑な関数近似をしなければ分類や回帰ができない場合、従来の機械学習手法ではうまくいかないケースも多いです。
そういった問題に対して、ディープラーニング手法を使用するケースが増えています。
ディープラーニングとは、隠れ層が多数存在する多層構造のニューラルネットワークのことを指します。
ディープラーニング手法は、分類問題や、回帰問題でよく使われます。
e.g. 回帰問題
- 結果予想(売上予想、株価予想など)
- ランキング(競馬順位予想、人気順位予想など)
e.g. 分類問題
- 猫写真の判別
- 手書き文字認識
- 花の種類分類
確認テスト
- ディープラーニングは、結局何をやろうとしているのか?
⇨ルールベースではなく、データから学習して回帰や分析などのタスクを行なうこと。
- どの値の最適化が最終目的か?
⇨重み[\(W\)]、バイアス[\(b\)]
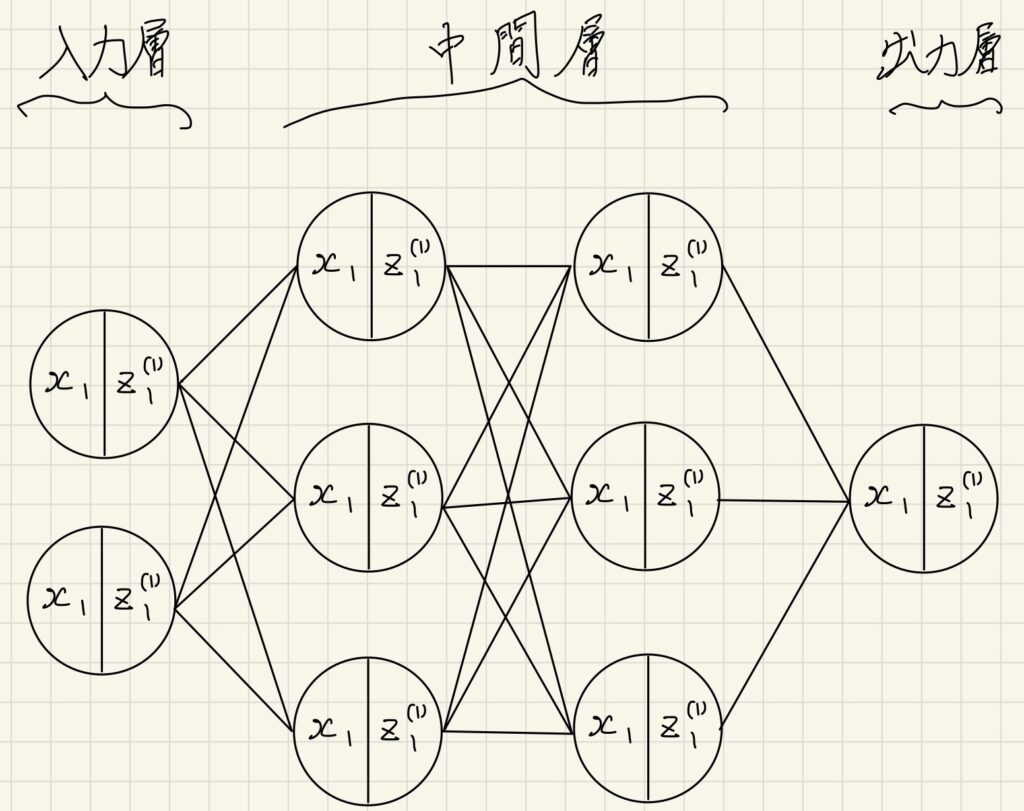
- 次のネットワークを紙に書け。
入力層:2ノード1層
中間層:3ノード2層
出力層:1ノード1層
入力層〜中間層
確認テスト
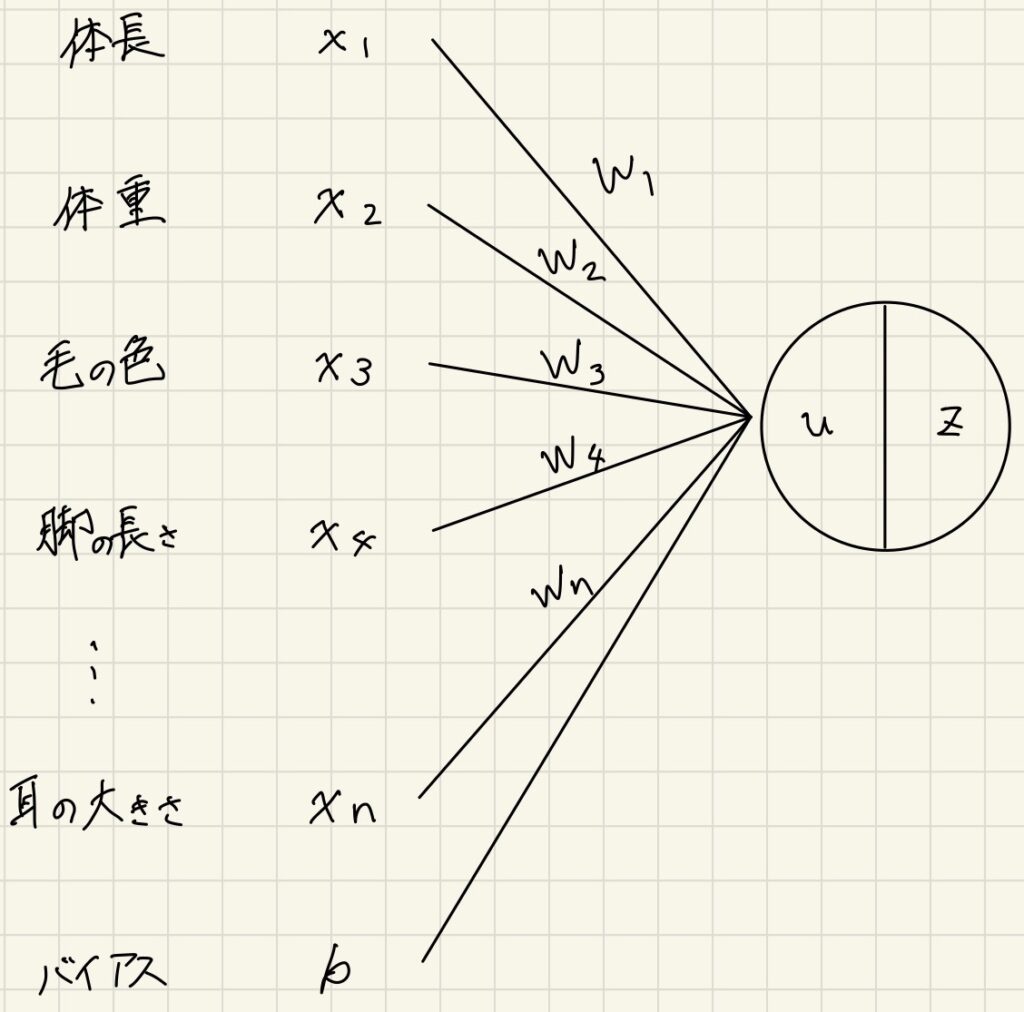
- 動物分類の実例を入れた図式の作成
- 次の数式をPythonで書け。
$$
\begin{align}
u&=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+b \\
&=Wx+b
\end{align}
$$
import numpy as np
u = np.dot(x, W) + b
- 「1_1_forward_propagation.ipynb」のファイルから中間層の出力を定義しているソースを抜き出せ。
z2 = functions.relu(u2)活性化関数
活性化関数とは、ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数のことです。
入力値によって、次の層への信号のON/OFFや強弱を定める働きを持ちます。
中間層に用いられる活性化関数
ステップ関数
関数への入力値が0未満の場合には常に出力値が0、入力値が0以上の場合には常に出力値が1となるような関数のことです。
0を基点(閾値)として、階段(step)状のグラフになるため、ステップ関数と呼ばれます。
$$
f(x)=
\begin{cases}
1 \ \ (x\ge0) \\
0 \ \ (x<0)
\end{cases}
$$
def step_function(x):
if x > 0:
return 1
else:
return 00〜1間を表現できず、線形分離可能なものしか学習できません。
シグモイド関数
0~1の間を緩やかに変化する関数です。
0~1の間で表現されるため、信号の強弱を伝えることができます。
$$
f(x)=\frac{1}{1+e^{-x}}
$$
def sigmoid(x):
return 1 / (1 + np.exp(-x))大きな値では、出力の変化が微小なため、勾配消失問題を引き起こすことがあります。
ReLU関数
最も使われている関数です。
入力が0より大きければそのまま出力し、0より小さければ0とします。
勾配消失問題の回避とスパース化に貢献することで、良い成果をもたらしています。
$$
f(x)=
\begin{cases}
x \ \ (x>0) \\
0 \ \ (x\le0)
\end{cases}
$$
def relu(x):
return np.maximum(0, x)確認テスト
- 「1_1_forward_propagation.ipynb」から活性化関数を使っている箇所を抜き出せ。
# 1層の総出力
z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)出力層
分類であれば各クラスに属する確率など、人が欲しい最終的な結果を出力します。
学習において、この出力層の結果と目的変数の値を比較し、どれくらい合っているかを算出するため誤差関数を用います。
誤差関数
例えば分類の場合、各クラスが属する確率とOne-hotベクトルで表現されている各クラスの正解値をもとに、どれだけ合っているか、ズレているか算出します。
誤差関数の値は、ズレているほど大きくなります。
二値分類ならクロスエントロピー関数、他クラス分類ならカテゴリカルクロスエントロピー関数、回帰なら平均二乗誤差や平均絶対誤差等が用いられます。
平均二乗誤差
def mean_squared_error(y, d):
return np.mean(np.square(y-d)) / 2クロスエントロピー関数
$$
E_{n}(w)=-\sum_{i=1}^{I}{d_{i}log\ y_{i}}
$$
def cross_entropy_error(d, y):
if y.ndim == 1:
d = d.reshape(1, d.size)
y = y.reshape(1, y.size)
#
if d.size == y.size:
d = d.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size確認テスト
- 平均二乗誤差において、なぜ二乗するのか。
⇨分散と同じ考え方のもと、プラスマイナスの値が混在していると、総和した際に正しく誤差を合計できないため。
- 平均二乗誤差において、なぜ1/2しているのか。
⇨式を簡略化するため。
二乗は微分すると2が係数として前に出てくるので、1/2をしておくことで打ち消すことができるから。
出力層の活性化関数
中間層と出力層で利用される活性化関数は異なります。
中間層の場合は、入力値の信号の強弱を重み付けするために用いられますが、出力層の場合は、信号の大きさはそのままに分類の確率や回帰の連続値等に変換します。
中間層用の活性化関数
- ReLU関数
- シグモイド(ロジスティック)関数
$$
f(x)=\frac{1}{1+e^{-x}}
$$ - ステップ関数
出力層用の活性化関数
- ソフトマックス関数
$$
f(i,u)=\frac{e^{u_{i}}}{\sum_{k=1}^{K}{e^{u_{k}}}}
$$
def softmax(x):
if x.ndim == 2:
x = x.T
x = x - np.max(x, axis=0)
y = np.exp(x) / np.sum(np.exp(x), axis=0)
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
- 恒等写像
- シグモイド(ロジスティック)関数
確認テスト
- ソフトマックス関数の数式に該当するコードについて、1行ずつ処理の説明をせよ。
def softmax(x):
if x.ndim == 2: # 2次元の場合
x = x.T # xを転置
x = x - np.max(x, axis=0) # xから列方向に取った最大値を引く
y = np.exp(x) / np.sum(np.exp(x), axis=0) # xの指数関数の値(数式の分子)を指数関数の総和(数式の分母)で割って確率としている
return y.T
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x))
- 交差エントロピー関数の数式に該当するコードについて、1行ずつ処理の説明をせよ。
def cross_entropy_error(d, y):
if y.ndim == 1: # 1次元の場合
d = d.reshape(1, d.size) # (1, 全要素数)のベクトルに変形
y = y.reshape(1, y.size) # (1, 全要素数)のベクトルに変形
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換する
if d.size == y.size:
d = d.argmax(axis=1) # argmaxで最大値のインデックスを取得
batch_size = y.shape[0] # 行の形状
# 「1e-7」は対数関数の結果が0になることを回避するために極めて小さい値を与えている
# np.arangeでバッチサイズ分取り出して対数関数に与えている
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7) / batch_size勾配降下法
勾配降下法とは、訓練テストに対してコストが最小になるように、モデルパラメータを少しづつ操作し、モデルを訓練テストに対して適合したパラメータに収束させる方法です。
勾配降下法にはいくつか種類があり、例えば次の3つなどがあります。
- 勾配降下法(バッチ勾配降下法)
- 確率的勾配降下法(SGD)
- ミニバッチ勾配降下法
| 手法 | 利用 データ | 計算 時間 | メリット | デメリット |
| バッチ勾配降下法 | 全て | 大 | ・解への到達が早いことが多い ・結果が安定する | ・メモリの使用量が多い ・局所解にハマりやすい |
| 確率的勾配降下法 | 1つ | 小 | ・メモリの使用量が少ない ・オンライン学習が可能 ・局所解を回避できる可能性がある | ・解への到達が遅いことがある ・外れ値の影響を大きく受ける |
| ミニバッチ勾配降下法 | 一部 | 中 | ・バッチ勾配降下法と確率的勾配降下法のそれぞれのメリットがある | ・バッチ勾配降下法と確率的勾配降下法のそれぞれのデメリットがある |
確認テスト
- 「1_3_stochastic_gradient_descent.ipynb」から次の数式に該当するコードを抜き出せ。
$$
w^{t+1}=w^{t}-\epsilon\Delta{E}
$$
network[key] -= learning_rate * grad[key]学習率
学習率は、パラメータの収束のしやすさのハイパーパラメータです。
学習率が大きいと、最適解を飛び越えて値が大きくなり、学習がうまく進まなくなります。このことを発散と呼びます。
逆に、学習率が小さいと発散する確率が減りますが、学習が終わるまでの時間がかかります。
また、学習率が小さいと、局所最適解(極小値)を求めてしまう可能性があります。
学習率を決定する手法は以下のような方法があります。
- Momentum
- AdaGrad
- Adadelta
- Adam
オンライン学習
オンライン学習とは、オンライン学習とは学習データが入ってくるたびにその都度、新たに入ってきたデータのみを使って学習する手法のことです。
バッチ学習と大きく異なるのは、学習を行う際に1からモデルを作り直すのではなく、そのデータによる学習で、今あるモデルのパラメータを随時更新していくという点です。
バッチ学習と比較して、オンライン学習の方がよく使われます。
以下、その特徴を挙げます。
- 1回の学習あたりのコストが低い
- 学習データをすべて蓄えておく必要がない
- ユーザー行動の変化にすぐ対応ができる
- 外れ値などノイズの影響を受けやすい
- 最新のデータの影響を受けやすい
確認テスト
- オンライン学習とは何か。
⇨上述の通りですが、モデルにその都度データ与えて学習させる学習手法です。学習データが入ってくる都度パラメータを更新し、学習を進めていきます。
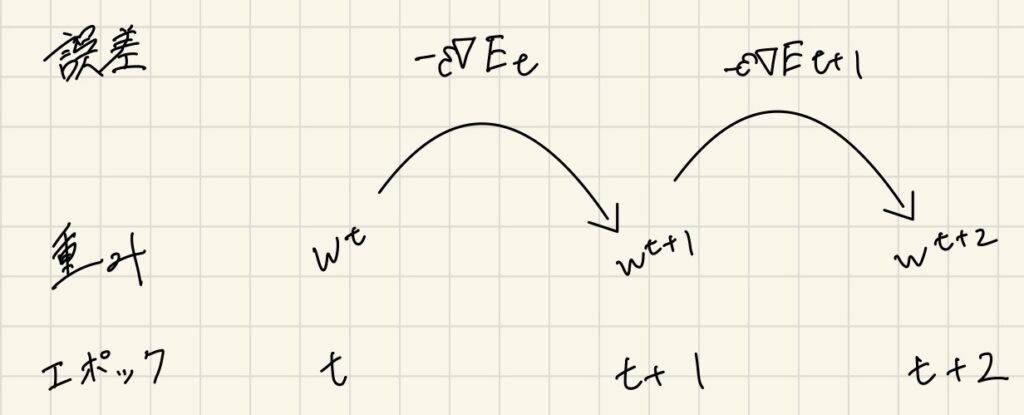
- 次の数式の意味を図に書いて説明せよ。
$$
w^{t+1}=w^{t}-\epsilon\Delta{E}
$$
前回のエポックの誤差を元に、重みを修正していくことによって、次のエポックではよりデータに適合した予測ができるようになっていきます。
誤差逆伝播法
誤差逆伝播法は、最小限の計算で各パラメータでの微分値を解析的に計算する手法です。
直接微分計算をすると、計算量が多くなってしまいます。
そこで、算出された誤差を出力層側から順に微分し、前の層へと伝播させていきます。
微分して前に戻していくことで、重みとバイアスを修正していきます。
計算の流れ
e.g. 入力層:1、中間層:1、 出力層:3のネットワークの場合
- 誤差関数(二乗誤差)\(E\)を\(y\)について微分します。
目的変数とのズレを見る誤差の計算から、活性化関数へ戻していく部分です。
$$
\frac{\partial E}{\partial y}=\frac{\partial}{\partial y}\frac{1}{2}||y-d||^2=y-d
$$
- 恒等関数を活性化関数に使用して出力します。\(y(u)\)を\(u\)について微分します。
活性化関数から出力層への部分です。
$$
\frac{\partial y(u)}{\partial u}=\frac{\partial u}{\partial u}=1
$$
- 中間層の出力から得られた入力\(z\)を元に\(w^{(I)}z^{(I-1)}+b^{(I)}\)で算出した\(u\)を\(w\)について微分します。
出力層から入力の部分です。
$$
\frac{\partial u}{\partial w_{ji}}=\frac{\partial}{\partial w_{ji}}(w^{(I)}z^{(I-1)}+b^{(I)})=\frac{\partial}{\partial w_{ji}}
\left(
\left[
\begin{array}{rrrrr}
w_{11}z_{i} & +…+ & w_{1i}z_{i} & +…+ & w_{1I}z_{I} \\
& & \vdots & & \\
w_{j1}z_{i} & +…+ & w_{ji}z_{i} & +…+ & w_{jI}z_{I} \\
& & \vdots & & \\
w_{J1}z_{i} & +…+ & w_{Ji}z_{i} & +…+ & w_{JI}z_{I} \\
\end{array}
\right]
+
\left[
\begin{array}{r}
b_{1} \\
\vdots \\
b_{j} \\
\vdots \\
b_{J} \\
\end{array}
\right]
\right)
=
\left[
\begin{array}{r}
0 \\
\vdots \\
z_{j} \\
\vdots \\
0 \\
\end{array}
\right]
$$
- 微分の連鎖率
$$
\frac{\partial E)}{\partial w_{ji}^{(2)}}=\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}=
(y-d)
\left[
\begin{array}{r}
0 \\
\vdots \\
z_{j} \\
\vdots \\
0 \\
\end{array}
\right]
=(y_{i}-d_{i})z_{i}
$$
微分の連鎖律によって1~3までの計算を掛け合わせることによって、誤差関数\(E\)を重み\(w\)で微分した結果を得られます。
\(w\)の(2)は2層目の中間層を示します。
確認テスト
- 誤差逆伝播法では不要な再帰的処理を避ける事が出来る。既に行った計算結果を保持しているソースコードを抽出せよ。
# 誤差逆伝播
def backward(x, d, z1, y):
# print("\n##### 誤差逆伝播開始 #####")
grad = {}
W1, W2 = network['W1'], network['W2']
b1, b2 = network['b1'], network['b2']
# 出力層でのデルタ(誤差関数を微分したもの)
delta2 = functions.d_mean_squared_error(d, y)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 中間層でのデルタ
#delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
## 試してみよう
# 誤差関数を微分した結果を前の層の計算にも使って戻していっている。
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
delta1 = delta1[np.newaxis, :]
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
x = x[np.newaxis, :]
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
# print_vec("偏微分_重み1", grad["W1"])
# print_vec("偏微分_重み2", grad["W2"])
# print_vec("偏微分_バイアス1", grad["b1"])
# print_vec("偏微分_バイアス2", grad["b2"])
return grad
- \(\frac{\partial E}{\partial y}\)に該当する「1_3_stochastic_gradient_descent.ipynb」のソースコードは次の通りです。
delta2 = functions.d_mean_squared_error(d, y)以下の2つの数式に該当するソースコードを探せ。
- \(\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\)
# z1について
z1, y = forward(network, x)
delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)
- \(\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}\)
grad['W1'] = np.dot(x.T, delta1)