はじめに
今回の記事は、前回に引き続き、私が受講しているE資格 JDLA認定プログラムの「ラビットチャレンジ」のレポート記事です。
今回のテーマは機械学習の主成分分析です。
コード実装を取り入れながら行っていきます。
主成分分析
主成分分析とは、多変量データの持つ構造をより少数個の指標に圧縮することです。
変量の個数を減らすことに伴う、情報の損失はなるべく小さくしながら、分析や可視化(2・3次元の場合)が実現可能になります。
学習データ
$$
x_{i}=(x_{i1},x_{i2},…,x_{im})\in\mathbb{R}^{m}
$$
平均(ベクトル)
$$
\bar{x}=\frac{1}{n}\sum_{i=1}^{n}{x_{i}}
$$
データ行列
$$
\bar{X}=(x_{1}-\bar{x},…,x_{n}-\bar{x})^T
$$
分散共分散行列
$$
\Sigma=Var(\bar{X})=\frac{1}{n}\bar{X}^{T}\bar{X}
$$
線形変換後のベクトル
$$
s_{j}=(s_{1j,…,s_{nj}})^T=\bar{X}a_{j} ~~~~~ a_{j}\mathbb{R}^{m}
$$
分散が大きい方が元のデータの情報を持っていると考えられるため、情報の量を分散の大きさと捉え、変換した後のデータの分散が最大となる射影軸を探索します。
分散共分散行列を使ったやり方以外にも相関行列を使った手法もあります。
ラグランジュ関数
目的関数
$$
arg~max~a_{j}^{T}Var(\bar{X})a_{j}
$$
制約条件
ノルムが1となる制約を入れます。
制約を入れないと無限に解が出てしまいます。
$$
a_{j}^{T}a_{j}=1
$$
ラグランジュ関数
ラグランジュ関数を最大にする係数ベクトル(微分して0になる点)を探します。
$$
E(a_{j})=a_{j}^{T}Var(\bar{X})a_{j}-\lambda(a_{j}^{T}a_{j}-1)
$$
$$
\frac{\partial{E(a_{j})}}{\partial{a_{j}}}=2Var(\bar{X})a_{j}-2\lambda{a_{j}}=0
$$
$$
Var(\bar{X})a_{j}=\lambda{a_{j}}
$$
元のデータの分散共分散行列の固有値と固有ベクトルが、上記の制約付き最適化問題の解となります。
また、射影先の分散は固有値と一致します。
分散共分散行列は正定値対称行列なので、固有値は必ず0以上・固有ベクトルは直行になります。
\(k\)番目の固有値(昇順)並べ、対応する固有ベクトルを第k主成分と呼びます。
寄与率
第\(k\)主成分の分散の全分散に対する割合(第k主成分が持つ情報量の割合)のことです。
$$
c_{k}=\frac{\lambda_{k}}{\sum_{i=1}^{m}{\lambda_{i}}}
$$
第1~元次元分の主成分の分散は、元のデータの分散と一致します。
2次元のデータを2次元の主成分で表示した時、固有値の和と元のデータの分散が一致します。
第\(k\)主成分の分散は主成分に対応する固有値になります。
累積寄与率
第1-\(k\)主成分まで圧縮した際の情報損失量の割合のことです。
$$
r_{k}=\frac{\sum_{j=1}^{k}{\lambda_{i}}}{\sum_{i=1}^{m}{\lambda_{i}}}
$$
実装演習
2次元のデータを2次元上に次元圧縮した際に、うまく判別できるかを確認していきます。
使用するデータ
Breast Cancer Wisconsinのデータを使用します。(乳がんに関するデータ)
https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29
必要なライブラリのインポート
import pandas as pd
import numpy as np
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
%matplotlib inlineデータの確認
今回のデータは、scikit-learnのdatasetsモジュールにあるload_breast_cancer()でデータを取得できます。
データはBunchクラスのオブジェクトです。
以下のコードでデータ構造を取得します。
cancer_ds = load_breast_cancer()
for key, value in zip(cancer_ds.keys(), cancer_ds.values()):
print("{}:\n{}\n".format(key, value))データのキーは以下のようになっています。
print(cancer_ds.keys())
# 出力
dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])data(特徴量データセット)
569人の細胞診結果に対する30個の特徴量のデータを格納した2次元配列。
列のインデックス(0~29)が30個の特徴量に対応しています。
target(診断結果に対応したコード)
各被検者の診断結果(悪性:malignant、良性:benign)を格納した0/1のコードの配列。
569個の腫瘤に対応した1次元配列(0:悪性が212、1:良性が357)です。
target_names(診断結果)
悪性(malignant)、良性(benign)が定義されています。
feature_names(特徴名)
細胞診の結果得られた30個の特徴量の名前です。
腫瘤に関する10の属性について、それぞれ平均(mean)、標準偏差(error)、最悪値(worst)の3種類、合計30の特性値に対する名前が格納されています。ここでworstは各属性に関する最大値となっています。
次に、pandasでデータを確認してみます。
df_target = pd.DataFrame(cancer_ds["target"], columns=["target"])
df_data = pd.DataFrame(cancer_ds["data"], columns=cancer_ds["feature_names"])
df = pd.concat([df_target, df_data], axis=1)
df # 一部省略して表示しています
データの前処理
主成分分析にかける前に、データの前処理をしていきます。
個々の特徴量を平均が0で分散が1になるように変換します。
# 目的変数の抽出
y = df["target"]
# 説明変数の抽出
X = df.loc[:, "mean radius":]
# 学習用とテスト用でデータを分離
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
# 標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)主成分分析
それでは、主成分分析で2成分に次元圧縮をします。
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)
print(pca.explained_variance_ratio_)
# 出力
[0.43315126 0.19586506]
# データを主成分空間に写像
df_pca = pd.DataFrame(X_train_pca, columns=["PC{}".format(x+1) for x in range(2)])
df_pca['Outcome'] = y_train.values # 分類結果も表に併せる
df_pca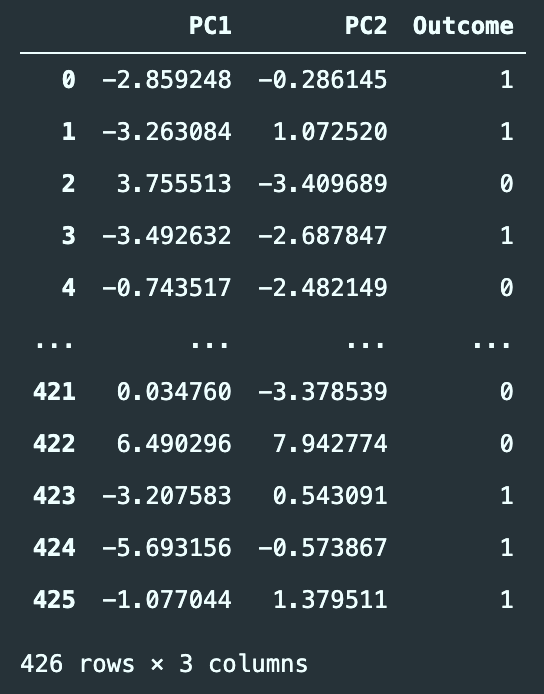
次に、散布図にプロットしてみます。
m = df_pca[df_pca['Outcome'] == 0]
b = df_pca[df_pca['Outcome'] == 1]
plt.scatter(x=m['PC1'], y=m['PC2'], label='malignant', c='r', marker='x', alpha=0.5)
plt.scatter(x=b['PC1'], y=b['PC2'], label='benign', c='b', marker='x', alpha=0.5)
plt.legend()
plt.xlabel('PC 1')
plt.ylabel('PC 2')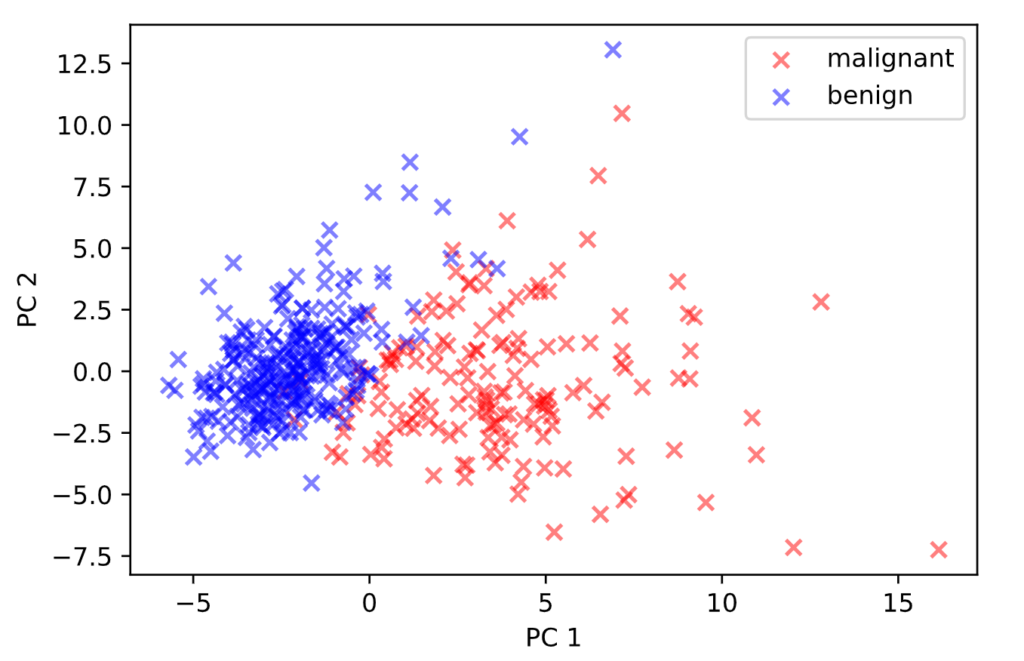
この2つの主成分のグラフを見ると、malignantとbenignがおおよそ分離出来ていることが分かります。